Teorema de Pitágoras

O teorema de Pitágoras leva o nome do matemático grego Pitágoras (570 a.C. – 495 a.C.). Segundo os historiadores, Pitágoras viajou para a Babilônia e Egito, vindo a fixar-se no sul da Itália (em Crotona), fundando a chamada Academia Pitagórica que lecionava, Matemática, Filosofia, Música e outras Ciências. O teorema que tradicionalmente é creditado à Pitágoras, porém, temos conhecimento que Pitágoras esteve na Babilônia, onde há muitas evidências de que matemáticos Babilônicos conheciam algoritmos para calcular os lados em casos específicos, mas, não se sabe se conheciam um algoritmo tão geral quanto o teorema de Pitágoras.  Assim, podemos ponderar o seguinte:  Pitágoras adaptou de forma didática o que aprendeu com outros e, conseguiu demonstrar de maneira simples e prática, de modo que todos pudessem aprender. Foi Pitágoras o primeiro a elevar a ciência dos números e da geometria à categoria das artes maiores e a estabelecer o princípio de que uma proposição científica deve ser totalmente convincente, isto é, verdadeiramente demonstrada. Existem inúmeras demonstrações do teorema de Pitágoras. Em 1940 o matemático americano Elisha Scott Loomis compilou 367 demonstrações diferentes para o seu livro "The Pythagorean Proposition". O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo retângulo. o teorema afirma que:

" Em todo triângulo retângulo o quadrado da Hipotenusa é igual a soma dos quadrados dos Catetos", cujos lados são: Cateto Oposto e Cateto Adjacente "

 

Por definição, a hipotenusa é o lado oposto ao ângulo, O enunciado anterior relaciona comprimentos, mas o teorema também pode ser enunciado como uma relação entre áreas: Para ambos os enunciados, pode-se equacionar:

 

Onde c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados. No exemplo acima o 3 elevado ao quadrado é = 9. O 4 elevado ao quadrado é = 16. E,  9+16 = 25. Como descobrir o comprimento da Hipotenusa?  O comprimento será a raiz quadrada do Quadrado da Hipotenusa. 

no exemplo acima, o comprimento da Hipotenusa é de 5 metros.

O teorema de Pitágoras, foi aplicado pelo matemático persa Ghiyath al-Kashi (1380 – 1429), lei dos cossenosque, permite o cálculo do comprimento do terceiro lado de qualquer triângulo. Conhecendo os comprimentos de dois lados e a medida de apenas um dos três ângulos. " Foi um matemático e astrônomo persa a quem é atribuído o desenvolvimento do teorema lei dos cossenos e a realização do cálculo da constante 2π com 9 dígitos sexagesimais de precisão. Ghiyath al-Kashi, foi considerado o Segundo Ptolomeu. Com o domínio dos Sassânidas, reis persas (Ciro e Xerxes) que, governaram a mesopotâmia, esta recuperou sua posição central ao longo das rotas comerciais, visto que sob o domínio Romano e Heleno haviam perdido. Não há muitos registros Sassânidas desta época. O que se sabe é que, era uma cultura muito rica, haja vista, o conto “Mil e uma noites” de Omar Khayyam. Depois da conquista árabe, em 641 teve origem a cidade de Bagdá, em substituição à Babilônia, que havia desaparecido. A matemática do período islâmico revela a mesma mistura de influências que se tornaram familiares em Alexandria e na Índia. A matemática e a astronomia foram grandemente incentivadas pelos Califas de Bagdá: Al-mansur (754-775), Harun Al-raschid (766-809) e Al-mamun (813-833). Este último organizou em Bagdá a “casa da sabedoria”, composta de uma biblioteca e um observatório. As atividades matemáticas árabes começaram com a tradução dos Siddanthas hindus por Al-Fazari e culminaram com uma grande importância com Muhammad Ibn Musa Al-Khwarizmi, por volta de 825. Ele escreveu vários tratados sobre matemática e astronomia. Estes tratados explicavam o sistema de numeração hindu. A europa ficou conhecendo este sistema de numeração graças a uma cópia latina do século XII, visto que o original Árabe se perdeu. A astronomia de Al-Khwarizmi era um resumo dos Siddanthas, o qual mostrava uma influência grega nos textos sânscritos. Convém ressaltar que a palavra “álgebra” vem do Árabe “al-jabr”, que siginifica “restauração”. Os Árabes tiveram um papel muito importante na história da matemática, pois eles traduziram, fielmente, os clássicos Gregos (Apolônio, Arquimedes, Euclides, Ptolomeu e outros). Estes clássicos estariam perdidos para nós sem os Árabes, visto o fechamento da escola de Atenas por Justiniano. Outro matemático brilhante foi Omar Khayyam. Ele escreveu uma álgebra que continha uma investigação sistemática de equações cúbicas, utilizando a interseção de duas seções cônicas. Jemshid Al-Kashi, matemático Persa resolveu equações cúbicas por interação e por métodos trigonométricos, e também pelo método conhecido hoje como “método de Horner”. Este método tem uma forte influência chinesa, o que nos faz pensar que a matemática chinesa da dinastia Sung havia penetrado profundamente no mundo islâmico. Por tudo isto, ressalta-se a importante influência do povo Árabe na matemática. É importante ressaltar que, os muçulmanos ao expandir o islamismo cometeram um dos maiores crimes contra a humanidade. Após a queda de Alexandria frente aos muçulmanos, o califa mandou queimar todos os manuscritos encontrados na biblioteca (cerca de 600.000) argumentando que: “se constam do alcorão não precisam ser guardados e se não constam são inúteis”. Conta a lenda que os escritos alimentaram as caldeiras dos banhos públicos, durante seis meses. É preciso lembrar também, o papel das cruzadas. Com as cruzadas a Europa cristã teve, novamente, contato com a matemática grega, traduzida para o Árabe. Isto veio a influenciar muito a Europa Medieval e serviu como fonte para o desenvolvimento da matemática durante a idade média".

Como calcular alturas e distâncias utilizando o Teodolito e Trigonometria

O teodolito é um instrumento capaz de medir ângulos,  ele é muito usado por agrimensores, engenheiros e topógrafos no cálculo de distâncias inacessíveis. Este instrumento ótico mede ângulos horizontais e verticais com suas duas escalas circulares graduadas em graus. A trigonometria serve para resolver o seguinte problema:
Para calcular a altura de um prédio, o topógrafo colocou seu teodolito na praça em frente e, mediu a distância do prédio ao teodolito com uma trena e encontrou 27 metros. Mirando o alto do prédio, ele verificou na escala do teodolito, que o ângulo formado por essa linha visual com a horizontal é de 58 graus. Se a luneta do teodolito está a 1,5 m do chão, qual é a altura do prédio? (seno) sen 58o = 0,85 e (coseno) cos 58o = 0,53. Para calcular use a Calculadora, Casio-FX-82MS e use as funções sen, cos e tan.

Solução: A trigonometria (trigono=triângulo + metria=medida) é o ramo da matemática que trata das relações entre os lados e ângulos de triângulos. No triângulo retângulo temos: Seno = Cateto Oposto ao ângulo, dividido pela Hipotenusa. Cosseno = Cateto Adjacente ao ângulo, dividido pela Hipotenusa. Cateto Oposto dividido pelo Cateto Adjacente é = Tangente.

 

Na figura abaixo temos:  AB, CD = 1,5m que corresponde a altura do solo atá a luneta do Teodolito. CE = X (onde X é a altura do prédio). CE + 1,5m do Teodolito é a altura do prédio. No triângulo retângulo formado pelos pontos BDE, BE é a hipotenusa , DE = X  é o cateto oposto ao ângulo de 58 graus, BD = 27m é o cateto adjacente ao ângulo de 58 graus. Trabalhando com as razões trigonométricas seno, cosseno e tangente, temos:

 

tg 58o = X ÷ 27m. Como, tg 58o = sen 58o ÷ cos 58o = 0,85 ÷ 0,53 = 85 ÷ 53 = 1,6 aproximadamente, podemos ter a proporção: 

X ÷ 27m = 0,85 ÷ 0,53 = 1,6.

Então temos no final: X = 27m × 1,6 = 43,2. Assim, a altura do prédio é : 43,2 + (altura do Teodolito) 1,5m = 44,7 metros.

Para concluir, podemos afirmar genericamente que, para encontrar a altura de um determinado objeto, basta saber apenas a Tangente. Pois multiplicando a tangente pelo comprimento Adjacente, temos a altura do objeto.

---

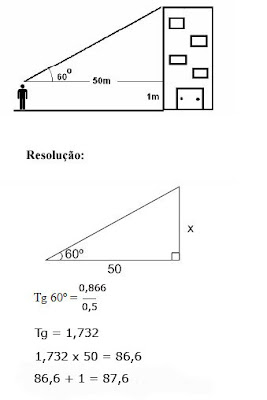
Exemplo 2: Calcular a altura de um prédio.

Primeiro, verifique se o nivelamento do solo está perfeito com a base do tripé do teodolito. Posicione e mire o Teodolito até encontrar um ponto de referência no TOPO do Prédio que você quer medir.

Veja o ÂNGULO associado à essa medida no Teodolito ou Transferidor e, anote. (no exemplo 60graus). Usando uma trena meça a DISTÂNCIA (m), entre o centro do Teodolito e o Prédio que você quer calcular a altura e, anote. Usando os princípios de Trigonometria calcule usando a altura do Prédio  a expressão abaixo. Adicione à altura calculada e encontrada, à altura do visor do Teodolito, aqui é de 1 metro.

sen de 60  é  = 0,866
cos de 60o  é  = 0,5
tg de 60o é = 1,732
(sen)0,866 ÷ (cos)0,5 =  (tg) 1,732 aproximadamente. Podemos ter a proporção: X ÷ 50m = 0,866 ÷ 0,5 = 1,732.

No final: X = 50m × 1,732 = 86,6. Assim, a altura do prédio é: 86,6 + (altura do Teodolito) 1m =  87,6 metros.

Para concluir, podemos afirmar genericamente que, para encontrar a altura de um determinado objeto, basta saber apenas a Tangente, e, multiplicando a tangente pelo comprimento Adjacente, temos a altura do objeto.

 

Adicionamos na altura encontrada + a altura da luneta do Teodolito que é, 1 metro. Assim, encontraremos a altura do prédio.